Which Best Explains Whether Point G Can Be the Centroid

Segment FG measures 6 cm and and segment FC measures 18 cm. Where μ ij is the membership value of point x i to centroid c j and d ij is the Euclidean distance of x i and c jLet U j μ 1j μ 2j μ Kj 7Therefore U U 1 U 2 U N denotes the membership value matrix and C c 1 c 2 c K denotes the cluster centroids set.

Ipad Apps Geometry Designer Illustration Circle Of Van Lamoen Triangle Medians Centroid Six Circum Education Math Education Education Technology Teachers

Given in triangle ABC the segments drawn from vertices intersect at point G.

. Answer 1 of 17. With μ yj and σ j computed on the sample sequence z 1 z n. The point corresponding to the geometric center of an object is known as the centroid.

Of a triangle lies at the point where all the three medians intersect each other. Correct answer to the question Point g is the centroid of the right abc with hypotenuse ab18 in. FG 6 cm FC 18 cm.

And also FC FG GC 18 6 GC GC 12. That is the point G will be 23 the distance from C to M. Segment FG measures 6 cm and and segment FC measures 18 cm.

W m represents the compactness as well as the uniformity measure of clusters. The correct explaination is Point G can be the centroid because 126 equals 21. In triangle abc the segments drawn from the vertices intersect at point g.

If we draw a line through these points we can see all the points lie on the same line. Find CD and CE. In general a smaller W m.

CG 23 9 in. The centroid of any triangle is at the intersection of medians which is 13 the distance along the median from the side to the vertex. Given in triangle ABC the segments drawn from vertices intersect at point G.

CG 6 in. 18 6 GC GC 12. Point g cannot be the centroid because fg should be longer than cg.

Which best explains whether point G can be the centroid. Centroid or centre of gravity of simple plane figures. Which best explains whether point g can be the centroid.

If a shape possesses an axis of symmetry then its centroid will always be located on that axis. Point G is the centroid H is the orthocenter and J is the circumcenter. CM is a median of ABC.

The correct explaination is Point G can be the centroid because 126 equals 21. Segment FG measures 6 cm and and segment FC measures 18 cm. Point g cannot be the centroid because 18.

In triangle ABC the segments drawn from the vertices intersect at point G. Given in triangle ABC the segments drawn from vertices intersect at point G. Therefore we can conclude that the centroid orthocenter and circumcenter are collinear.

Ratio of GC to FG is 126 21. If it has two axes of symmetry then the interse. In Exercises 4 and 5 point D is the centroid of AABC.

CM 18 in2 9 in. Point G can be the centroid because 126 equals 21. The NC classifier computes centroids for each class and for a new example will predict the class with the nearest centroid based on a given distance metric.

And also FC FG GC. FG 6 cm FC 18 cm. FG 6 cm FC 18 cm.

As two straight lines can intersect in only one point 55 O is the only point that can be the center of a circle through the three given points. 18 6 GC GC 12. Of a uniform rod lies at its middle point.

Depending on the shape of the object one two or three coordinates may be needed in order to define its exact position in space. The centroid is 23 of the distance along the median away from the vertex and so it is 13 of the distance away from point D the midpoint of. DE 7 5.

Answer to Solved In Exercises 4 and 5 point D is the centroid of. And also FC FG GC. Point g can be the.

Notice that FC FG GC which means that GC FC - FG 18 - 6 12cm. If it has one axis of symmetry the controls will be in that axis. Therefore the statement that best explains whether point G can be the centroid is Point G can be the centroid because 126 equals 21.

Point G can be the centroid because 126 equals 21. Of a rectangle or a parallelogram or a square lies at. Centroid of an object is the geometric centre.

ϕ NC x 0 y 0 j z 1 z n x 0 j - μ y. DE 12 CD-4A CD는 ercises 6-8 find the coordinates of the centroid of the triangle with the given In Ex vertices. Centre of gravity is the point where the total weight of the body acts while centroid is the geometric centre of the object.

The correct explaination is Point G can be the centroid because 126 equals 21. Segment fg measures 6 cm and segment fc measures 18 cm. 6 does not equal 2.

Segment FG measures 6 cm and segment FC measures 18 cm. 160 The center of any circle that passes through the three points must be in both of these perpendicular bisectors andhence at their intersection. Below mentioned is the construction part.

Given that segmentFG measures 6 cm and segment FC measures 18 cm. Centre of gravity or centre of mass is the point where the whole mass of the body is concentrated. This is where the gravitational force weight of the body acts for any orientation of the body.

Using Euclidean distance a plausible NCM is given by. In engineering if you need to find the centre of an object we use centroid. The centroid is a very simpler concept.

Centroid Of A Triangle Formula Properties Examples

Centroid Of A Triangle Math Tricks Math Triangle

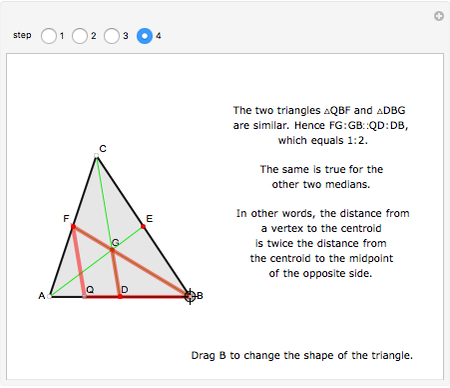
The Centroid Of A Triangle Divides Each Median In The Ratio 1 2 Wolfram Demonstrations Project